Elasticity: the grail of Revenue Management. Elusive. Yet it’s sold to us as a simple formula: e = dQ/dP. It’s nice, it’s simple, but it’s wrong.
This formula or similar formulations can be found everywhere, on Wikipédia as well as on websites talking about economics or MR. So once and for all, why is it wrong?
Elasticity, the example of the hotel industry
Take a hotel with 400 rooms. An expected occupancy rate of 200, with a price of €100. Expected turnover of €20,000 (€100 x 200).
Assuming that the elasticity is known, that it is -1.5 (which means that if we lower the price by 10%, we will have 15% more demand), what are the consequences? Let’s run some tests:
- Price -10% / Volume +15%. Turnover = €20,700 (€90 x 230)
- Price -15% / Volume +22.5%. Turnover = €20,825 (€85 x 245)
- Price -20% / Volume +30%. Sales = €20,800 (€80 x 260)
Turnover initially rises as prices fall, then falls again. Why does this happen? Remember the maths from secondary school: it’s because sales describe a negative parabola (like the trajectory of a pebble when you throw it in front of you).
Mathematically, it is a function of the 2nd degree which can be written CA(x) = P * V (1+x) * (1+ex), where x is the price variation, P and V the initial price and volume, e the elasticity. An ex² function, with negative e.
If the elasticity is less than -1, which everyone agrees is the case (with a few exceptions), this function reaches its maximum at a single point, like a pebble that is thrown and reaches its peak somewhere. This single point is obtained when the derivative of the function is zero. This is the case when x takes the value -(e+1)/2e (the derivative is zero when 2ex + e+1 = 0. In our example, with an elasticity of -1.5, the value of x that maximises sales is -0.5/6 = -17%).
We would therefore need to give a discount of 17% to maximise sales. This is the optimum. After that, you go home because any other action would destroy value. That’s the best we can do.
Going further, this calculation gives us the complete equation producing the « optimal value » of discount that would maximise turnover for each elasticity value (as long as the volume generated remains within capacity limits). We could then draw up a curve of optimal values: this is the function f(e) = -(e+1)/2e which varies according to the elasticity e.
Curiously, this curve tends towards -50% when elasticity tends towards infinity (in the negative). This would mean, another absurdity, that whatever the starting point, no situation can lead to an improvement in sales for a discount of more than 50%.
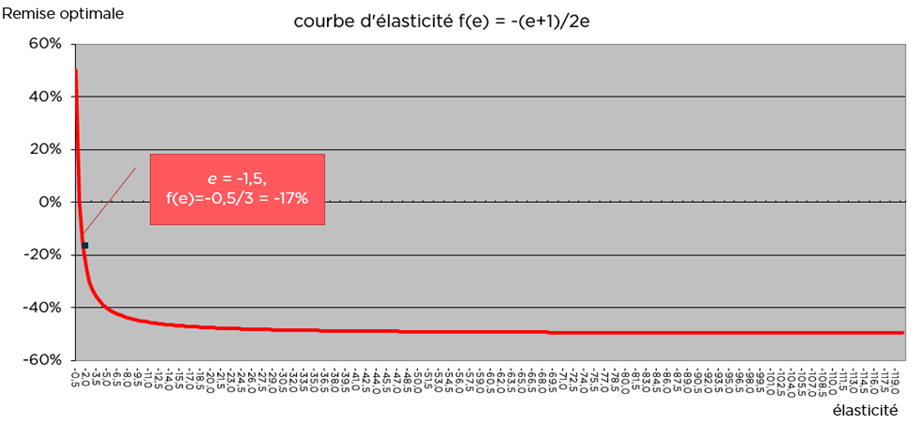
Elasticity curve
But why isn't this true?
This is what the elasticity function tells us if we assume that it is e=dQ/dP. Because we haven’t made any additional assumptions. We’ve just written the equation that follows, and taken the reasoning all the way.
It is clear that this is false and that there is no such thing as an « optimal discount » or an « optimal price » that would maximise turnover once and for all.
This is false because elasticity is much more complex.
It varies according to the initial price, the lead time, the market, the sales channel, the type of customer and the product purchased. The level of granularity is one of the problems. We need to cross-reference all these dimensions, but then we have too few points of observation. And then the calculation has to stay close to the starting point to be accurate, on very small variations. But in the accommodation business, we’re not at the petrol pump. Prices vary enormously. It’s hard to imagine a price cut of 0.04%.
What’s more, the demand response to a price cut is not the same depending on how the price is packaged (in terms of value, slashed price, % discount, free nights, etc.) and how it is communicated (highlighting, marketing budget for advertising, etc.).
And then there are exogenous effects: response from competitors, cannibalisation effects on substitute products, etc.
To go further and put an end to elasticity, we invite you to read our previous article on the subject.
In short, reducing elasticity to a simplistic equation and trying to profit from it is absurd. With very few exceptions, elasticity is not only impossible to measure but also very difficult to manipulate.
The RM has a thousand smarter things to do. And trying to achieve this holy grail, which is more for show than for effective Yield management, is not one of them.
Keywords: Elasticity, Revenue Management, volume, optimal value, turnover


